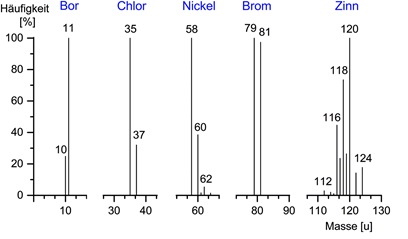
Diese ergibt sich aus der Summe der Massenzahlen aller beteiligten Atome des jeweils konkret betrachteten Moleküls (bezogen auf die häufigste Masse der Isotope der Elemente). Sie ist immer ganzzahlig.
Die meisten Elemente kommen in der Natur als Gemische verschiedener Isotopen definierter Zusammensetzung vor (polyisotopische Elemente). Die Molmasse (auch Molekülmasse oder Molekulargewicht) wird berechnet als der gewichtete Mittelwert der natürlich vorkommenden Isotope eines Element.
Als Isotope bezeichnet man Nuklide in ihrem Verhältnis zueinander, wenn ihre Atomkerne gleich viele Protonen (gleiche Ordnungszahl), aber verschieden viele Neutronen enthalten. Sie stellen dann ein und dasselbe Element dar, verhalten sich also chemisch weitgehend identisch, haben aber verschiedene Massenzahlen.
Die exakte Masse eines beliebigen Isotops ist mit der Ausnahme von 12C, dem Bezugsisotop der Atommassenskala, immer geringfügig verschieden vom nominellen Wert. Beispielsweise ist die exakte Masse von 1H nicht 1 u sondern 1,007825 u und die von 16O nicht 16 u sondern 15,994915 u.
Die Ursache für den Massendefekt liegt in der Äquivalenz von Masse und Energie (E = mc2), welche sich darin ausdrückt, dass Isotope mit sehr stabilen Kernen bei ihrer Bildung mehr Energie pro Nukleon freisetzen – und damit an Masse verlieren – als Kerne leichter Elemente.
Da man sich auf 12C bezieht, haben die leichteren Elemente mit geringerer Kernbindungsenergie pro Nukleon exakte Isotopenmassen leicht über dem nominellen Wert, während schwerere Elemente alle etwas darunter liegen.
Als monoisotopische Masse eines Ions wird die isotopische Masse desjenigen Isotopen-Ions bezeichnet, das ausschließlich aus den häufigsten natürlichen Isotopen der einzelnen beteiligten Elementen zusammengesetzt ist. Sind die häufigsten Isotope der Elemente einer Verbindung ausschließlich auch deren leichtesten, so entspricht die Masse des Ions, das beim kleinstem m/z-Wert registriert wird, der monoisotopischen Masse. Das entsprechende Ion ist das monoisotopische Ion.
Bei hochmolekularen Verbindungen weicht die monoisotopische Masse stark von deren nominalen Masse ab.
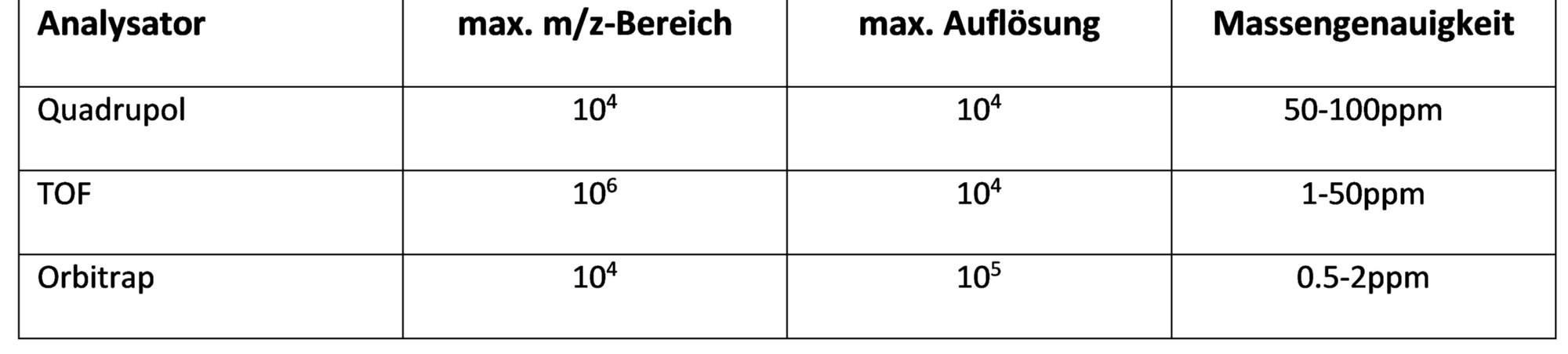
Die Qualität der Massentrennung wird als Massenauflösung (oder kurz Auflösung R) bezeichnet, die Fähigkeit eines Analysators eine entsprechende Trennung zu erzielen, heißt Auflösungsvermögen.
Man definiert Auflösung R, bzw. Auflösungsvermögen aus dem Verhältnis der Signalbreite oder eines Massenabstands, Δm, zur Masse, m, bei der dieser Wert erreicht wird:
R= m/∆m
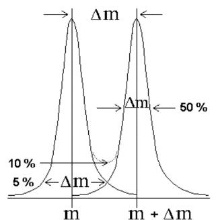
Zur Bestimmung der Auflösung bzw. des Auflösungsvermögens misst man die Breite eines Signals bei 5 % seiner Intensität. Da sich Intensitäten benachbarter Peaks im Überlappungsbereich addieren, ergibt sich daraus eine Trennung bis auf einen Taleinschnitt von 10 % der Intensität. Man nennt dies die 10 %-Tal-Definition der Auflösung (R10 %). Bei Peaks mit Δm/z = 1 ist der Abstand zwischen den Peakmaxima gleich der Peakbreite bei 10 % der Intensität.
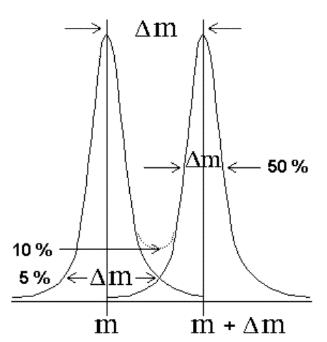
Häufig wird auch die Peakbreite bei halber Höhe als Δm verwendet. Das ist die 50 %-Tal-Definition der Auflösung (full width at half maximum, FWHM), mit der man ca. 1,8-mal höhere Werte bei gleicher Peakform errechnet. Um Peaks zu trennen, ist als Auflösungsvermögen immer der Zahlenwert der Masse des Ions erforderlich, d. h. Rmin = 1500 bei m/z 1500.
Gemeinhin werden Spektren mit Werten von R < 2000 als niedrig aufgelöste und solche mit R > 5000 als hochaufgelöste Spektren bezeichnet; der Übergangsbereich ist nicht wirklich definiert.
Eine hohe Auflösung ist vor allem auch bei mehrfach geladenen Makromolekülen sehr wichtig, da die Differenzen der m/z-Verhältnisse im Isotopenmuster mit steigender Ladung proportional abnehmen.
Beispiel: Isotopenmuster des zweifach negativ geladenen Oligonukleotid 8-mer T8 als Profilspektren.
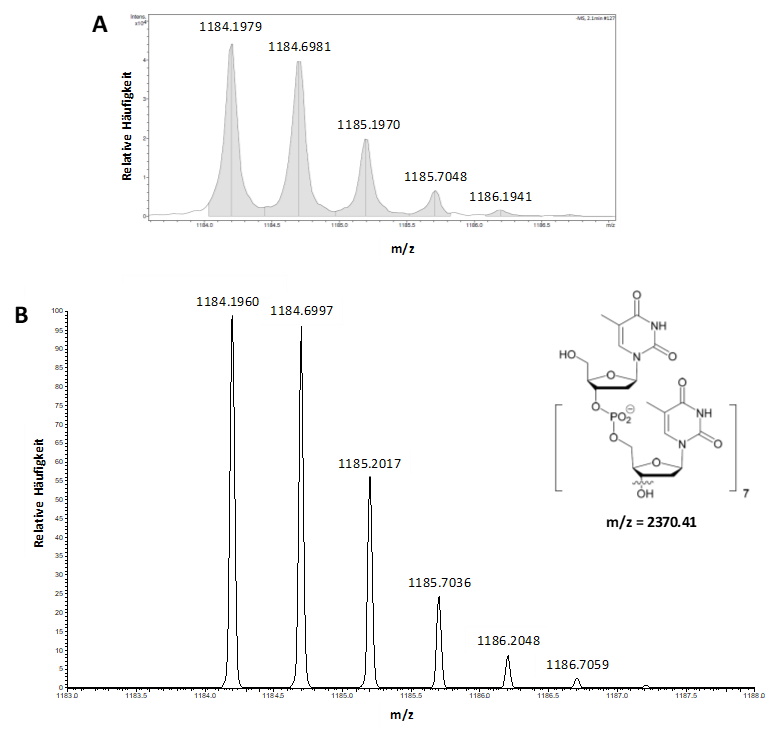Gemessen: A) ESI-Q-TOF R= 15.000 (FWHM) B) Exactive Plus Orbitrap R=100.000 (FWHM); bei B) Basislinientrennung!
Die Massengenauigkeit ist relevant für die Ermittlung der Summenformel aus einer exakten Masse. Man definiert die absolute Massengenauigkeit Δm/z und die relative Massengenauigkeit in Bruchteilen der Masse; meist angegeben in Parts-per-Million (ppm).
Die absolute Massengenauigkeit hochauflösender Massenspektrometer liegt heute oft bei 1–3 Millimassen, die relative Massengenauigkeit bei 1–5 ppm. Allerdings bleibt die absolute Massengenauigkeit über einen großen Bereich konstant, während der Zahlenwert der relativen Massengenauigkeit linear von der Masse abhängt. So entsprechen ± 0.002 Δm/z einer Abweichung von 2 ppm bei m/z 1000 aber 20 ppm bei m/z 100.
Eine hohe Massengenauigkeit ist u.a. bei komplexen Metallverbindungen sehr wichtig, da dabei einige Elemente mehrere stabile Isotope aufweisen können.
Beispiel: Isotopenmuster des Cs2Mo6Br8Cl6-Clusters gemessen an verschiedenen Massenspektrometern.
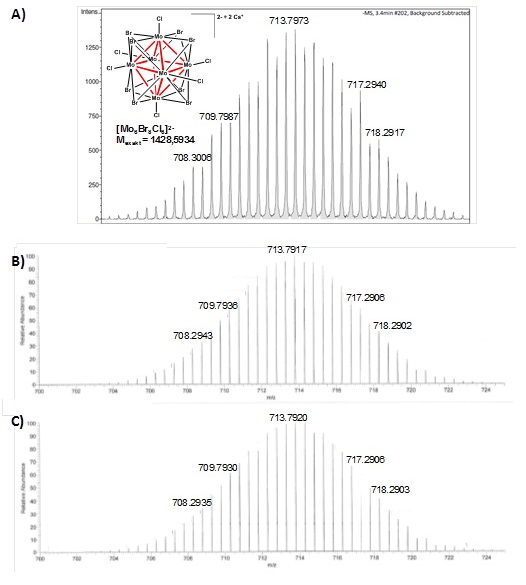
A) Profilspektrum; ESI-Q-TOF; 8ppm B) Profilspektrum; Exactive Plus Orbitrap; <1ppm C) Simuliertes Isotopenmuster des Clusters.
Die um den Faktor 10 höhere Massengenauigkeit ist im Falle dieses Clusters, in dem alle Elemente mehrere stabile Isotope aufweisen, von entscheidender Bedeutung für die eindeutige Bestimmung der Elementarzusammensetzung (stabile Isotope Molybdän: 92Mo, 94Mo, 95Mo, 96Mo, 97Mo, 98Mo, Chlor: 35Cl, 37Cl und Brom: 79Br, 81Br).
Die Empfindlichkeit ist ein weiterer wichtiger Parameter. Sie ist jedoch auch vom Analyten abhängig und kann daher nicht allgemein angegeben werden. Sie ist als Steigung der Kalibrierkurve (von Signal gegen Konzentration) definiert.
Die Empfindlichkeit kann durch die Addition von Einzelspektren (scans) zu einem Gesamtspektrum verbessert werden. Bei der Addition von X scans verbessert sich das S/N (Signal-Rausch-Verhältnis) mit √𝑋.
Denn das Signal der Messsubstanz kehrt in jedem scan wieder, die Signale des Rauschens verteilen sich statistisch (mal auf der einen, mal auf der anderen Masse). Das Signal S muss mindestens 5x grösser als das chemische Rauschen N sein.
Die Anzahl der möglichen Zusammensetzungen von Ionen hängt in hohem Maße vom m/z-Wert des Ions ab. Selbst wenn man nur die Ionen mit gerader Elektronenzahl und nur die Elemente C, H, N, O betrachtet, gibt es abhängig von der relativen Massengenauigkeit, bei hohen Massen, eine große Auswahl an möglichen Summenformeln für des gemessene Ion.
Die eindeutige Zuordnung von Summenformeln allein auf der Grundlage der exakten Masse gelingt meist nur in einem Bereich bis zu m/z 500. Danach übersteigt die Anzahl der Treffer bei Ionen mit größeren m/z-Werten, selbst bei einer hohen Massengenauigkeit von 1 ppm, jegliches praktikable Maß.
Es wird noch komplizierter, wenn man zusätzliche Elemente berücksichtig. Deshalb muss man versuchen, sich auf bestimmte Elemente zu beschränken und wenn möglich die maximale und/oder minimale Anzahl bestimmter Isotope einzuschränken.
Zusatzinformationen kann man auch durch die Isotopenmuster erhalten. Einige Elemente haben sehr eindeutige Isotopenverteilungen. (z.B. S, B, Cl, Br, einige Metalle...)
Wenn man die Informationen aus den exakten Messdaten und experimentell ermittelten Peakintensitäten mit berechneten Isotopenmustern kombiniert, lässt sich die Anzahl der potenziellen Summenformeln signifikant reduzieren.
